Domain Of A Graph Calculator

Learning Outcomes

Discover domain and range from a graph, and an equation.
Give the domain and range of the toolkit functions.

Another way to identify the domain and range of functions is by using graphs. Considering the domain refers to the ready of possible input values, the domain of a graph consists of all the input values shown on the [latex]x[/latex]-axis. The range is the set of possible output values, which are shown on the [latex]y[/latex]-axis. Continue in mind that if the graph continues beyond the portion of the graph nosotros can see, the domain and range may be greater than the visible values.

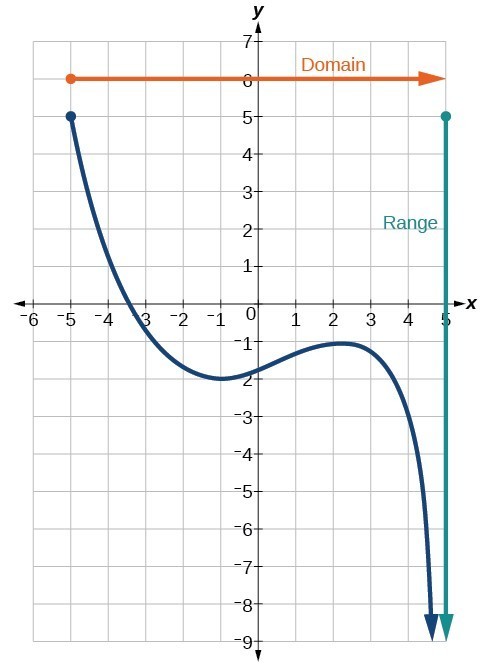
Graph of a polynomial that shows the x-axis is the domain and the y-axis is the range

We can find that the graph extends horizontally from [latex]-v[/latex] to the correct without bound, so the domain is [latex]\left[-v,\infty \correct)[/latex]. The vertical extent of the graph is all range values [latex]five[/latex] and below, then the range is [latex]\left(\mathrm{-\infty },five\right][/latex]. Notation that the domain and range are ever written from smaller to larger values, or from left to right for domain, and from the bottom of the graph to the top of the graph for range.

Instance: Finding Domain and Range from a Graph

Find the domain and range of the function [latex]f[/latex].

Graph of a function from (-3, 1].

Example: Finding Domain and Range from a Graph of Oil Production

Find the domain and range of the function [latex]f[/latex].

Effort It

Given the graph, place the domain and range using interval notation.

Graph of World Population Increase where the y-axis represents millions of people and the x-axis represents the year.

Show Solution

Domain = [latex][1950, 2002][/latex] Range = [latex][47,000,000, 89,000,000][/latex]

Q & A

Tin can a function's domain and range be the same?

Yep. For example, the domain and range of the cube root part are both the fix of all real numbers.

Domain and Range of Toolkit Functions

We will now return to our set of toolkit functions to make up one's mind the domain and range of each.

Constant function f(x)=c.

For the abiding part [latex]f\left(x\right)=c[/latex], the domain consists of all real numbers; in that location are no restrictions on the input. The only output value is the constant [latex]c[/latex], and then the range is the gear up [latex]\left\{c\right\}[/latex] that contains this single element. In interval notation, this is written as [latex]\left[c,c\correct][/latex], the interval that both begins and ends with [latex]c[/latex].

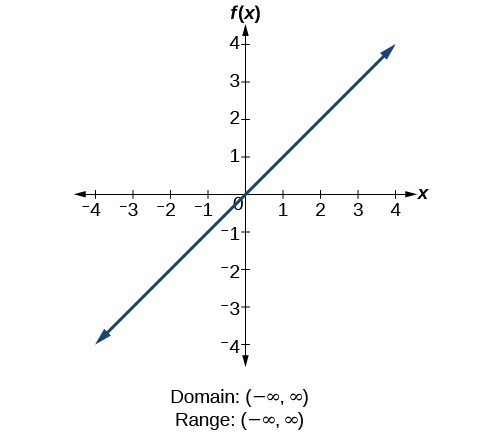
Identity function f(x)=x.

For the identity function [latex]f\left(x\right)=x[/latex], at that place is no restriction on [latex]10[/latex]. Both the domain and range are the set of all real numbers.

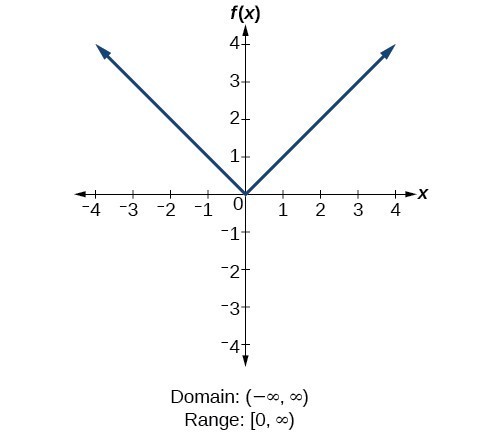
Absolute function f(x)=|x|.

For the absolute value function [latex]f\left(ten\right)=|x|[/latex], there is no restriction on [latex]x[/latex]. However, considering accented value is defined as a altitude from 0, the output tin just be greater than or equal to 0.

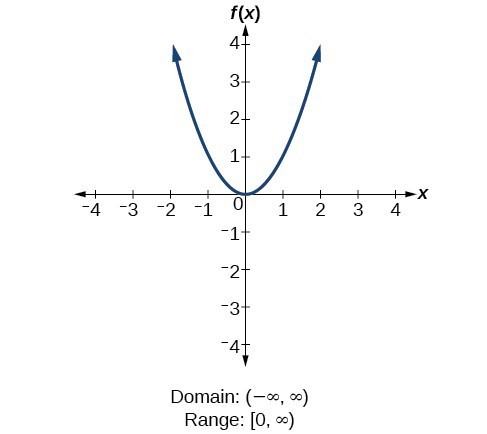
Quadratic function f(x)=x^2.

For the quadratic function [latex]f\left(x\correct)={x}^{2}[/latex], the domain is all real numbers since the horizontal extent of the graph is the whole existent number line. Because the graph does not include any negative values for the range, the range is only nonnegative existent numbers.

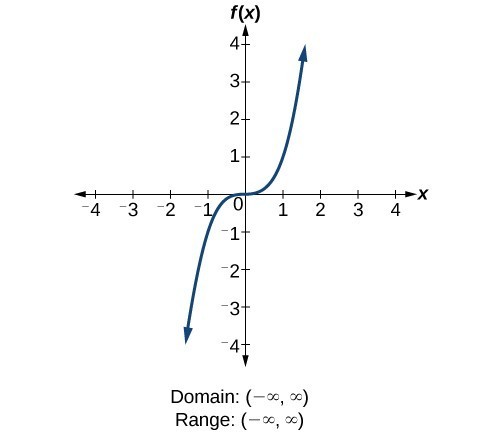
Cubic function f(x)-x^3.

For the cubic function [latex]f\left(x\right)={x}^{3}[/latex], the domain is all existent numbers because the horizontal extent of the graph is the whole real number line. The same applies to the vertical extent of the graph, so the domain and range include all real numbers.

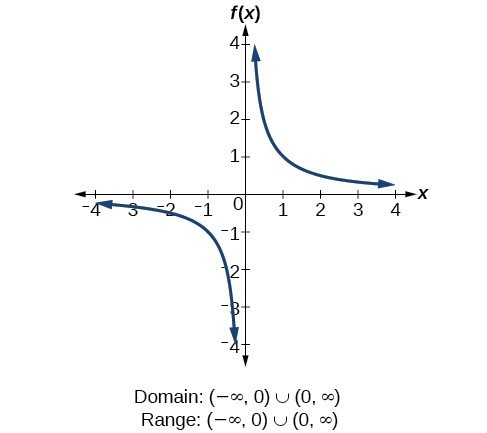
Reciprocal function f(x)=1/x.

For the reciprocal function [latex]f\left(x\right)=\frac{1}{x}[/latex], we cannot separate past 0, and then we must exclude 0 from the domain. Further, 1 divided by any value tin never be 0, and so the range also will not include 0. In set-architect notation, we could also write [latex]\left\{ten|\text{ }x\ne 0\right\}[/latex], the set of all real numbers that are not zero.

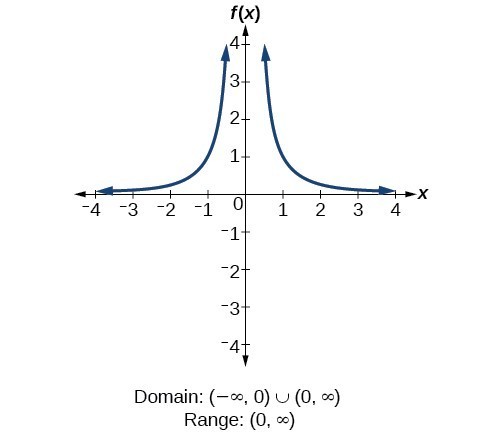
Reciprocal squared function f(x)=1/x^2

For the reciprocal squared office [latex]f\left(x\right)=\frac{1}{{x}^{2}}[/latex], we cannot dissever by [latex]0[/latex], so we must exclude [latex]0[/latex] from the domain. There is also no [latex]ten[/latex] that can give an output of 0, so 0 is excluded from the range likewise. Note that the output of this role is always positive due to the square in the denominator, and then the range includes merely positive numbers.

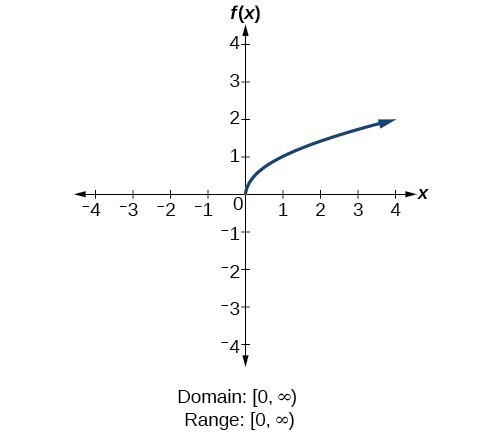
Square root function f(x)=sqrt(x).

For the foursquare root function [latex]f\left(10\right)=\sqrt[]{x}[/latex], we cannot accept the square root of a negative real number, so the domain must exist 0 or greater. The range as well excludes negative numbers because the square root of a positive number [latex]10[/latex] is defined to be positive, even though the square of the negative number [latex]-\sqrt{x}[/latex] besides gives us [latex]x[/latex].

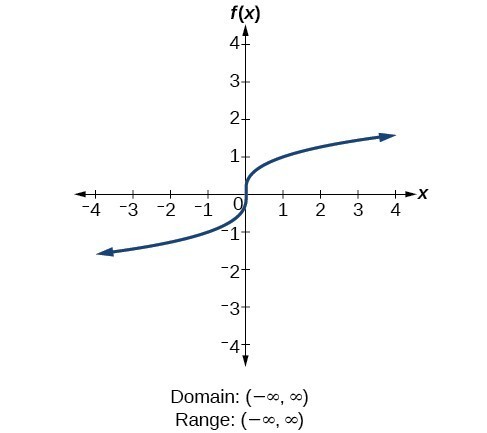
Cube root function f(x)=x^(1/3).

For the cube root part [latex]f\left(ten\right)=\sqrt[three]{x}[/latex], the domain and range include all real numbers. Annotation that there is no trouble taking a cube root, or any odd-integer root, of a negative number, and the resulting output is negative (information technology is an odd function).